এই লেখাটি পড়লে আপনি জানতে পারবেন সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র সম্পর্কে বিস্তারিত সবকিছু। জ্যামিতি আমাদের চারপাশের পৃথিবীকে বোঝার জন্য একটি গুরুত্বপূর্ণ হাতিয়ার। এর মধ্যে সামান্তরিক একটি অত্যন্ত গুরুত্বপূর্ণ আকৃতি, যা জমির হিসাব থেকে শুরু করে স্থাপত্যকলা পর্যন্ত বিভিন্ন ক্ষেত্রে ব্যবহৃত হয়। এই নিবন্ধে আমরা সামান্তরিক কী, এর বৈশিষ্ট্য, পরিসীমা নির্ণয়ের সূত্র এবং বাস্তব জীবনে এর ব্যবহার নিয়ে বিস্তারিত আলোচনা করব। এই লেখাটি ছাত্র-ছাত্রী এবং সাধারণ জিজ্ঞাসুদের জন্য সহজ ও স্পষ্টভাবে উপস্থাপন করা হয়েছে।
সামান্তরিক কাকে বলে জানুন
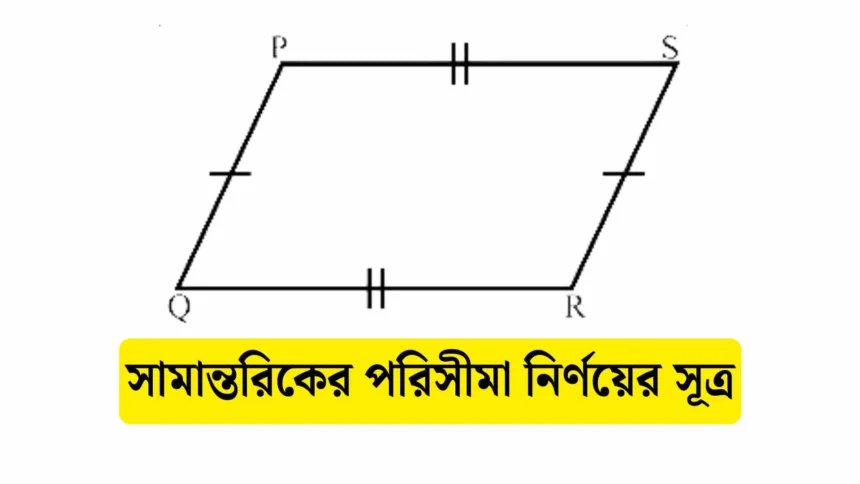
সামান্তরিক হলো এমন একটি চতুর্ভুজ (চারটি বাহুবিশিষ্ট আকৃতি), যার বিপরীত বাহুগুলো একে অপরের সমান এবং সমান্তরাল। উদাহরণস্বরূপ, ধরুন ABCD একটি সামান্তরিক। এখানে AB বাহু DC বাহুর সমান এবং সমান্তরাল, এবং AD বাহু BC বাহুর সমান এবং সমান্তরাল। এই বৈশিষ্ট্যই সামান্তরিককে অনন্য করে।
সামান্তরিকের প্রধান বৈশিষ্ট্য যা যা
একটি চতুর্ভুজকে সামান্তরিক বলতে হলে নিম্নলিখিত বৈশিষ্ট্য থাকতে হবে:
- বিপরীত বাহু সমান: সামান্তরিকের বিপরীত বাহুগুলোর দৈর্ঘ্য একই হয়। যেমন, AB = DC এবং AD = BC।
- বিপরীত বাহু সমান্তরাল: বিপরীত বাহুগুলো কখনো একে অপরকে ছেদ করে না। অর্থাৎ, AB || DC এবং AD || BC।
- বিপরীত কোণ সমান: সামান্তরিকের বিপরীত কোণগুলোর পরিমাপ সমান। যেমন, ∠DAB = ∠BCD এবং ∠ABC = ∠ADC।
- সন্নিহিত কোণের যোগফল ১৮০°: পাশাপাশি থাকা দুটি কোণের যোগফল সবসময় ১৮০°। যেমন, ∠DAB + ∠ADC = ১৮০°।
- কর্ণের বৈশিষ্ট্য: সামান্তরিকের দুটি কর্ণ একে অপরকে মাঝখানে ছেদ করে এবং সমান দুই ভাগে ভাগ করে।
সামান্তরিকের পরিসীমা সম্পর্কে জানুন
পরিসীমা হলো কোনো আকৃতির চারপাশের সীমানার মোট দৈর্ঘ্য। সামান্তরিকের ক্ষেত্রে, এটি হলো চারটি বাহুর দৈর্ঘ্যের যোগফল। উদাহরণস্বরূপ, যদি আপনি একটি সামান্তরিক আকৃতির মাঠের চারপাশে হাঁটেন, তবে আপনি যে মোট দূরত্ব অতিক্রম করবেন, তা-ই হলো পরিসীমা।
সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র
সামান্তরিকের বিপরীত বাহুগুলো সমান হওয়ায় পরিসীমা বের করতে শুধু দুটি সন্নিহিত বাহুর দৈর্ঘ্য জানা প্রয়োজন। ধরা যাক, একটি সামান্তরিকের দুটি সন্নিহিত বাহুর দৈর্ঘ্য যথাক্রমে a এবং b। তাহলে পরিসীমা নির্ণয়ের সূত্র হলো:
P = 2 × (a + b)
এখানে:
- P = পরিসীমা
- a = এক জোড়া বিপরীত বাহুর দৈর্ঘ্য
- b = অন্য জোড়া বিপরীত বাহুর দৈর্ঘ্য
এই সূত্রটি চারটি বাহুর যোগফলকে (a + b + a + b) সহজভাবে প্রকাশ করে।
ধাপে ধাপে পরিসীমা নির্ণয়
- বাহুর দৈর্ঘ্য জানুন: সামান্তরিকের দুটি সন্নিহিত বাহুর দৈর্ঘ্য পরিমাপ করুন।
- দৈর্ঘ্য যোগ করুন: দুটি বাহুর দৈর্ঘ্য (a + b) একসঙ্গে যোগ করুন।
- যোগফলকে ২ দিয়ে গুণ করুন: ফলাফলকে ২ দিয়ে গুণ করলেই পরিসীমা পাওয়া যাবে।
ব্যবহারিক উদাহরণ
উদাহরণ ১: দুটি বাহুর দৈর্ঘ্য জানা থাকলে
ধরা যাক, একটি সামান্তরিকের দুটি সন্নিহিত বাহুর দৈর্ঘ্য যথাক্রমে ১৫ সেমি এবং ১০ সেমি। এর পরিসীমা কত?
সমাধান:
- দেওয়া আছে: a = ১৫ সেমি, b = ১০ সেমি
- সূত্র: P = 2 × (a + b)
- P = 2 × (১৫ + ১০) = 2 × ২৫ = ৫০ সেমি
ফলাফল: পরিসীমা ৫০ সেমি।
উদাহরণ ২: পরিসীমা ও একটি বাহুর দৈর্ঘ্য জানা থাকলে
একটি সামান্তরিক আকৃতির জমির পরিসীমা ১২০ মিটার এবং একটি বাহুর দৈর্ঘ্য ৪০ মিটার। অন্য বাহুর দৈর্ঘ্য কত?
সমাধান:
- দেওয়া আছে: P = ১২০ মিটার, a = ৪০ মিটার
- সূত্র: P = 2 × (a + b)
- ১২০ = 2 × (৪০ + b)
- ১২০ ÷ ২ = ৪০ + b
- ৬০ = ৪০ + b
- b = ৬০ − ৪০ = ২০ মিটার
ফলাফল: অন্য বাহুর দৈর্ঘ্য ২০ মিটার।
পরিসীমা বনাম ক্ষেত্রফল এর পার্থক্য
পরিসীমা এবং ক্ষেত্রফল প্রায়ই গুলিয়ে ফেলা হয়। নিচের সারণিতে তাদের মধ্যে পার্থক্য স্পষ্ট করা হলো:
| বৈশিষ্ট্য | পরিসীমা (Perimeter) | ক্ষেত্রফল (Area) |
|---|---|---|
| সংজ্ঞা | আকৃতির চারপাশের সীমানার মোট দৈর্ঘ্য। | আকৃতির ভেতরের মোট জায়গার পরিমাণ। |
| একক | মিটার (m), সেন্টিমিটার (cm) ইত্যাদি। | বর্গমিটার (m²), বর্গসেন্টিমিটার (cm²) ইত্যাদি। |
| সূত্র | P = 2 × (a + b) | ক্ষেত্রফল = ভূমি × উচ্চতা |
| ধারণা | এক-মাত্রিক (1D) পরিমাপ। | দ্বি-মাত্রিক (2D) পরি� direto2D পরিমাপ। |
বাস্তব জীবনে সামান্তরিকের পরিসীমার ব্যবহার
- কৃষিকাজ: জমিতে বেড়া দেওয়ার জন্য কতটা তার লাগবে, তা জানতে পরিসীমা হিসাব করা হয়।
- নির্মাণ শিল্প: বাড়ির ফ্লোরপ্ল্যানে স্কার্টিং বা বর্ডার লাগাতে কতটা উপকরণ প্রয়োজন, তা পরিসীমা দিয়ে নির্ণয় করা হয়।
- খেলাধুলার মাঠ: কিছু খেলার মাঠ সামান্তরিক আকৃতির হয়। এর সীমানা চিহ্নিত করতে পরিসীমা ব্যবহৃত হয়।
- ডিজাইনিং: পোশাক বা অন্যান্য নকশায় বর্ডার বা লেস লাগানোর জন্য পরিসীমা হিসাব করা প্রয়োজন।
সাধারণ ভুল এবং সমাধান
- ভুল: শুধু দুটি বাহুর দৈর্ঘ্য যোগ করা (a + b)।
- সমাধান: যোগফলকে অবশ্যই ২ দিয়ে গুণ করতে হবে।
- ভুল: পরিসীমা এবং ক্ষেত্রফলের সূত্র গুলিয়ে ফেলা।
- সমাধান: মনে রাখুন, পরিসীমা হলো বাইরের দৈর্ঘ্য, আর ক্ষেত্রফল হলো ভেতরের জায়গা।
- ভুল: এককের অমিল (যেমন, একটি বাহু মিটারে এবং অন্যটি সেন্টিমিটারে)।
- সমাধান: সব পরিমাপ একই এককে রূপান্তর করে হিসাব করুন।
প্রায়শই জিজ্ঞাসিত প্রশ্ন (FAQ)
প্রশ্ন: আয়তক্ষেত্র ও সামান্তরিকের পরিসীমার সূত্র কি একই?
উত্তর: হ্যাঁ, সূত্র একই। আয়তক্ষেত্র একটি বিশেষ সামান্তরিক, যার কোণ ৯০°। তাই এর পরিসীমা P = 2 × (দৈর্ঘ্য + প্রস্থ)।
প্রশ্ন: রম্বসের পরিসীমা কীভাবে বের করব?
উত্তর: রম্বসের চারটি বাহু সমান। তাই এর পরিসীমা P = 4 × a, যেখানে a যেকোনো বাহুর দৈর্ঘ্য।
শেষ কথা
সামান্তরিকের পরিসীমা নির্ণয় একটি সহজ কিন্তু অত্যন্ত গুরুত্বপূর্ণ গাণিতিক ধারণা। P = 2 × (a + b) এই সূত্রটি মনে রাখলে এবং এর পেছনের ধারণা বুঝলে যেকোনো পরিস্থিতিতে এটি সহজেই প্রয়োগ করা যায়। এই ধরনের শিক্ষা সম্পর্কিত খবর সবার আগে জানতে শিক্ষা নিউজের সোসাল মিডিয়াগুলোকে ফলো করুন।
শিক্ষা নিউজে শিক্ষা সম্পর্কিত সঠিক তথ্যের আপডেট সবার আগে জানতে শিক্ষা নিউজের সোসাল হ্যান্ডেলগুলো অনুসরণ করুন।
Discover more from Shikkha News | শিক্ষা নিউজ
Subscribe to get the latest posts sent to your email.